В наше время, когда осуществляются самые дерзновенные мечты о достижении космических просторов, когда созданные руками человека искусственные спутники и космические ракеты проникают в безбрежные дали солнечной системы, мысль человеческая устремляется в поиски новых, неизведанных путей овладения космосом. Люди не только мечтают, но и начинают математически рассчитывать возможность полета к другим звездам нашей Галактики. Как же преодолеть огромное расстояние, отделяющее от нас даже самые близкие звезды? Будущий астронавт сможет преодолеть его в течение человеческой жизни, только если его корабль будет двигаться со скоростью, близкой к скорости света.
Наблюдатель, движущийся с околосветовой (или, как говорят, релятивистской) скоростью, существует пока лишь на страницах фантастических романов. О фотонных ракетах хотя и пишут [см.], но твердой основы для их осуществления пока еще нет. Сможет ли когда-нибудь полет с релятивистской скоростью стать действительностью?
История науки и техники убедительно показывает, что самое категорическое «нет» нельзя распространять на будущее. То, что сегодня представляется невозможным, может завтра стать вполне осуществимым. Тем не менее, и в наши дни, при современном уровне знаний, можно предвидеть хотя бы часть тех трудностей и препятствий, с которыми встретится и которые должен будет преодолеть будущий релятивистский астронавт. Движение с релятивистской скоростью таит в себе ряд неожиданностей, о которых рассказывается в публикуемой статье.
Мы не собираемся затрагивать вопрос о том, как осуществить движение макроскопического тела с релятивистской скоростью. Допустим, что эта задача каким-то образом решена и релятивистский межзвездный корабль создан. И хотя мы знаем, что нет макроскопических тел, у которых скорость движения хотя бы в какой-то степени приближалась к скорости света, нам представляется все же любопытным и поучительным взглянуть на окружающий мир глазами пассажира релятивистского корабля.
Картина, которая представилась бы ему, будет довольно непривычной. Мы не встречали ее описания, и это вполне естественно: с сильно выраженными релятивистскими эффектами мы сталкиваемся пока только в в мире микрочастиц. Как изменится для нашего астронавта вид звездного неба и насколько иной будет видимая им картина небосвода? Как будет выглядеть звезда, мимо которой не на слишком большом от нее расстоянии пролетит релятивистский корабль? Как будет действовать на звездолет и его экипаж межзвездная среда — микрометеориты, пылевое вещество, межзвездный газ?
ВИД ЗВЕЗДНОГО НЕБА
Чтобы ответить на эти вопросы, следует вспомнить некоторые положения, вытекающие из специальной теории относительности.
Представим себе две системы. Одна из них «неподвижна», т. е. покоится относительно «неподвижных звезд», или же, подобно Солнцу и Земле, перемещается с обычными астрономическими скоростями в десятки и сотни километров в секунду.
Другая связана со звездолетом и движется относительно первой системы со скоростью, сравнимой со скоростью света. Существуют определенные соотношения между координатами и временем в обеих системах [прим.]. Из этих соотношений следует, что для движущегося наблюдателя свет отдаленной звезды приходит под несколько другим углом, чем для неподвижного. Это явление называется аберрацией. Кроме того, изменяется и наблюдаемая частота световых колебаний, в чем состоит так называемый эффект Допплера. В результате этих эффектов резко изменится вид звездного неба.
Представим себе, что для неподвижного наблюдателя небо усеяно звездами равномерно, как это показано на рис. 1, слева, где звезды расположены под углами 0°, 15°, 30°, ...165°, 180°. Вследствие аберрации мы получим новое видимое расположение тех же звезд для движущегося наблюдателя (рис. 1, справа), а именно: звезды сгущаются впереди звездолета и раздвигаются позади него. Если считать, что скорость звездолета составляет 0,866 от скорости света [прим.] (с = 300 000 км/сек), то вся передняя полусфера неподвижного наблюдателя умещается для астронавта в конусе с углом раствора 30° (см. рис. 1, справа). Если же скорость звездолета составит 0,95 от скорости света, то этот конус будет иметь угол раствора всего лишь около 18°.
Рис. 1. Вид звездного неба. Вверху, слева: таким привыкли видеть звездное небо жители Земли, движущиеся вместе с Землей с обычными астрономическими скоростями (десятки и сотни километров в секунду); внизу, слева: «нормальный» транспортир, градусы которого расположены равномерно. Так же «равномерно» усеяна звездами небесная сфера. Вверху, справа: для релятивистского астронавта, т. е. движущегося со скоростью 260 000 км/сек, близкой к скорости света, все звезды «сбегаются» к той точке, на которую держит курс ракета. Внизу, справа: «релятивистский» транспортир, градусная сетка стала такой, что в направлении движения ракеты прежний угол в 90° занимает теперь на небесной сфере только 30° «нормального» транспортира
Изменение расположения звезд еще не исчерпывает особенностей той картины неба, которая наблюдается визуально из движущейся системы, поскольку существенно изменяется и спектральный состав излучения. Существует только одно исключительное направление наблюдения, на котором такого изменения не произойдет. Если скорость звездолета составляет 0,866 от скорости света, то в покоящейся системе это направление составит с направлением полета звездолета угол в 54° 50', а в системе, движущейся с указанной скоростью,— угол 125° 10'. Для всех звезд, которые расположены под углом меньше 54° 50', произойдет уменьшение частот, т. е. все частоты излучаемого звездой света движущийся наблюдатель увидит смещенными в длинноволновую часть спектра (произойдет «красное» смещение). Для звезд, расположенных под углом больше 54° 50', частоты окажутся смещенными в коротковолновую часть («фиолетовое» смещение). Звезды, свет от которых приходит под углом 54° 50', сохраняют для движущегося наблюдателя такой же спектр, какой они имеют для неподвижного наблюдателя [прим.].
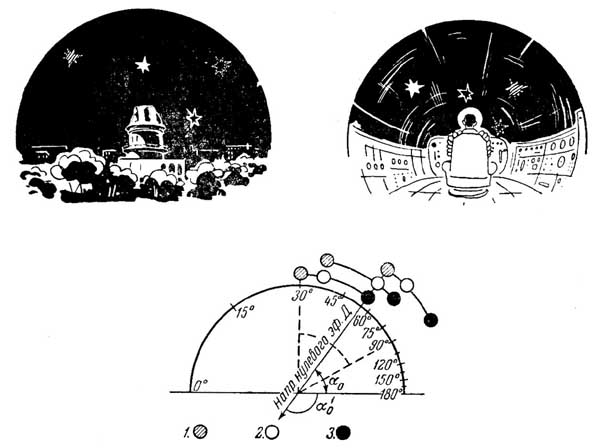
Рис. 2. Слева — для нас на этом небе сверкают звезды: красная (1), зеленая (2) и фиолетовая (3), четвертая, показанная пунктиром, невидима (инфракрасная). Справа — для астронавта блестят также три звезды, но все они сдвинулись к точке, на которую направлен нос ракеты, и изменили свой цвет: фиолетовая стала невидимой, зеленая — фиолетовой, красная — зеленой, а невидимая звезда сделалась красной. Внизу — если астронавт движется вправо и смотрит вдоль линии нулевого эффекта Допплера, то звезды, видимые по этому направлению, сохраняют для него привычный «земной» цвет. Если он посмотрит на звезды, расположенные немного ближе к курсу корабля, то увидит их с теми изменениями цвета, которые описаны выше. При наблюдении в направлениях, еще более близких к курсу корабля, все видимые цвета окажутся невидимыми — ультрафиолетовыми, а на их место придут «бывшие» инфракрасные
На рис. 2 показано, какой цвет приобретут звезды для наблюдателя, движущегося с вышеуказанной скоростью (0,866c), если они находятся не на направлении нулевого эффекта Допплера. Пусть в неподвижной системе звезда испускает свет с одной из трех длин волн видимого спектра, а именно: 4000 и 8000 Å (границы видимой области) и 5000 Å (зеленая линия). Тогда, если эта звезда находится вне конуса, показанного на рис. 2 пунктиром, то видимый для неподвижного наблюдателя свет сделается невидимым для астронавта, сместившись либо в сторону ультрафиолета, либо в сторону инфракрасных лучей. Если она расположена на направлении нулевого эффекта Допплера, то ее цвет не изменится. При отклонении же от этого направления, но в пределах конуса, показанного пунктиром, длины волн будут меняться так, как это показано на рис. 2 заштрихованными кружками.
Разумеется, произойдет и обратное явление: излучения, невидимые для неподвижного наблюдателя, попадут в видимую область спектра для астронавта. При том же значении скорости астронавт увидит позади себя источники, посылающие ультрафиолетовые волны длиной от 1070 до 2140 Å, а впереди — источники, посылающие инфракрасные волны длиной от 14950 до 29900 Å.
ИСКАЖЕНИЕ ФОРМЫ ВСТРЕЧНОЙ ЗВЕЗДЫ
Хорошо известно, что преобразование Лоренца приводит к продольному сокращению длин, так что сфера, проносящаяся мимо наблюдателя с релятивистской скоростью, оказывается заметно сплющенной в направлении движения, т. е. превращается в эллипсоид [прим.]. Эта конфигурация является истинной. Таково одновременное расположение точек движущейся сферы в какой-то момент времени по часам неподвижного наблюдателя. Нас же будет сейчас интересовать другой вопрос — не об одновременном истинном положении точек движущегося тела, а об их одновременном видимом положении. Это совсем другое, так как в каждый момент мы будем видеть разновременные положения точек движущегося тела. Происходит это потому, что свет, попадающий в глаз наблюдателя в один и тот же момент времени, тратит различное время на распространение от разных точек движущегося тела до глаза. Речь идет здесь, в сущности, снова о явлении аберрации, но в отличие от предыдущего раздела, нас интересуют теперь не бесконечно отдаленные источники, а источники, находящиеся на конечных расстояниях. Нетрудно рассчитать, как связаны между собой истинное и видимое положения такого точечного источника.
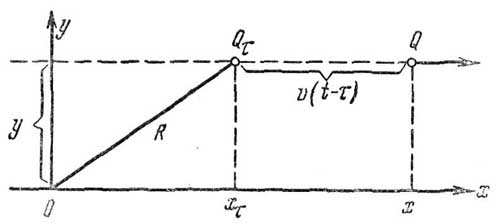
Рис. 3. Схема, поясняющая различие между истинным и видимым положениями точечного источника (буквенные обозначения см. в тексте)
Допустим теперь (физически это ничего не меняет, а рассуждения проше), что наблюдатель покоится в точке O системы K, а мимо него со скоростью υ проносится параллельно оси x, на некотором «прицельном расстоянии» y точечный источник (рис. 3). В момент времени t по часам К, когда источник находится в точке Q, наблюдатель видит его в предшествующем положении Qτ, которое источник занимал в момент τ < t, причем t — τ есть время распространения света из Q τ до O (t — τ = R/c). Таким образом, истинная абсцисса x и видимая абсцисса xτ различаются па отрезок υ(t — τ). Это позволяет для каждой точки тела, истинное положение которой в момент времени t известно, рассчитать видимое положение этой точки.
В какой-либо момент времени t по часам наблюдателя
K истинная конфигурация движущейся мимо него сферы — это (как следует из преобразования Лоренца) эллипсоид (т. е. в сечении плоскостью
x, y это эллипс с центром в точке х = υt,
у = а и с полуосями ρ
и ρ) (рис. 4)
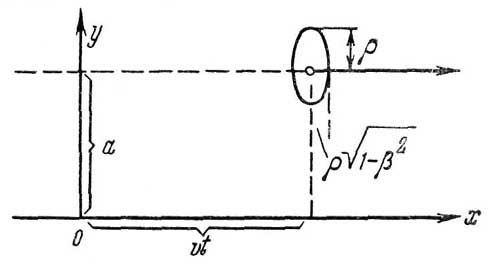
Рис. 4. Схема, поясняющая соотношение между осями истинного эллипса (буквенные обозначения см. в тексте)
Видимая конфигурация оказывается существенно отличной от истинной и меняется со временем.
Рис. 5. Два истинных положения движущейся сферы (пунктир) и соответствующие им видимые положения и конфигурации (сплошные кривые)
На рис. 5 изображены два истинных положения движущейся «сферы» (пунктирные кривые 1 и 2} и соответствующие им видимые положения и конфигурации (сплошные кривые 1 и 2). При построении принято, что расстояние между наблюдателем и траекторией центра сферы («прицельное расстояние») в пять раз превышает радиус сферы и что скорость равняется 0,866 от скорости света. Кривые 1 отвечают моменту времени, когда центр сферы находится против наблюдателя, а кривые 2 —моменту времени, когда центр фигуры виден против точки О.
В то время как истинная конфигурация представляет собой (в плоскости чертежа) равномерно движущийся эллипс с соотношением осей 1 : 2, видимая конфигурация — это овал, который по мере движения поворачивается и сильно меняет как свою форму, так и свою поступательную скорость. В дополнение к рис. 5 на рис. 6 показаны видимые фигуры, которые звезда имеет задолго до прохождения мимо наблюдателя и спустя достаточно большое время после этого.
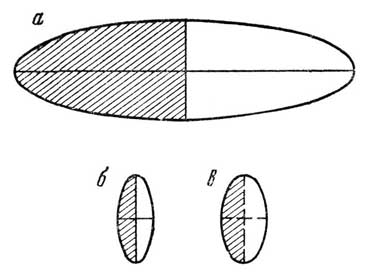
Рис. 6. Видимые конфигурации движущейся сферы. а — задолго до ее прохождения мимо наблюдателя; б — спустя большое время после встречи с ним; в — изображение истинного эллипса
Приближающаяся сфера, пока она еще достаточно далека, имеет форму вытянутого в направлении движения эллипсоида [прим.]. По мере приближения фигура несколько отходит от точной формы эллипса, сокращается и поворачивается острым концом к наблюдателю, о чем дают представление кривые 1 и 2 на рис. 5. Вместе с тем, сокращается отставание видимого положения от истинного и уменьшается кажущаяся скорость. Спустя достаточно большое время после встречи, сфера снова становится эллипсоидом, который теперь сплющен в направлении движения сильнее, чем истинный эллипсоид [прим.] (кривая в на рис. 6). Для скорости, равной 0,866 от скорости света, центр эллипсоида в каждый момент времени отстоит от наблюдателя на расстояние, примерно в два раза меньшее, чем в действительности, и удаляется с видимой скоростью, которая тоже примерно вдвое меньше истинной [прим.].
Разумеется, если известна истинная относительная скорость, то всегда может быть сделан пересчет к неподвижной системе и восстановлена действительная картина. Это относится как к конфигурации встречной звезды, так и к виду звездного неба в целом, о котором говорилось выше.
Указанные причудливые изменения формы проносящейся мимо звезды нельзя, однако, увидеть непосредственно, без измерения расстояний до различных точек ее поверхности. Проекция сложных фигур, о которых говорилось выше, на небесную сферу всегда остается круглым диском. Таким образом, релятивистское сжатие сферы в направлении ее движения при простом визуальном наблюдении не обнаруживается [прим.].
У проносящейся мимо звезды происходит, конечно, и изменение спектра ее излучения. При приближении она видна за счет своего инфракрасного излучения, в какой-то период времени при встрече длины волн проходят через их «покоящиеся» значения, а затем в видимую область спектра попадает ультрафиолетовое излучение звезды. Все это происходит не так уж быстро, если вспомнить, что свет пересекает земную орбиту примерно за 17 мин. При скорости 0,866c прохождение этого пути потребует около 20 мин., а по часам астронавта — около 10 мин.
РЕЛЯТИВИСТСКИЕ ПЫЛЬ И ВЕТЕР
Звездолет, двигаясь в космическом пространстве, находится во встречном потоке микро- и макрочастиц (межзвездный газ, микрометеорные тела и т. п.). Если пренебречь собственными скоростями этих частиц, то они налетают на звездолет со скоростью его движения. Можно вычислить, какую энергию получит звездолет при столкновении с частицами, находящимися в межзвездном пространстве. Оказывается, что при скорости 0,866c частица с массой 1 мг будет иметь кинетическую энергию в 21 млрд. калорий. Эта энергия достаточна для того, чтобы превратить в пар около 30 т льда или около 10 т железа. Импульс такой частицы будет равен при этом 520 кг·м/сек, т. е. будет примерно таким же, как у велосипедиста, едущего со скоростью 30 км/час.
Каких явлений можно ожидать при ударе микрометеорита о массивный корпус звездолета? Оценим, какова кинетическая энергия одного нуклона, входящего в состав микрометеорита, по сравнению с энергией связи этого нуклона в ядре атома.
При движении со скоростью 0,866c на один нуклон приходится энергия в 1 млрд. эВ, в то время как энергия связи нуклонов в ядрах (у элементов с атомным весом более 20) составляет лишь около 8 млн. эВ. Таким образом, можно полностью пренебречь не только энергией связи атомов в кристаллической решетке, но и энергией связи нуклонов в ядрах атомов — как в веществе метеорита, так и в материале звездолета. Это означает, что атомы микрометеорита врежутся в оболочку звездолета как некоторая группа тяжелых космических частиц, каждая из которых будет растрачивать свою энергию практически независимо от остальных.
Энергия в несколько млрд. электрон-вольт на нуклон соответствует «мягким» космическим лучам, т. е. длина пробега ядер железа, кремния и т. п., влетающих с такими скоростями в столь же плотные материалы, измеряется несколькими сантиметрами или немногими десятками сантиметров. После этого их энергия будет израсходована на образование еще более «мягких» частиц и в конечном счете будет поглощена корпусом звездолета вследствие больших ионизационных потерь. Таким образом, столкновение с микрометеоритом, имеющим массу в 1 мг, вызовет — при наличии на его пути достаточно большой массы металла — катастрофический тепловой взрыв всего корабля.
Разумеется, эффект, производимый более мелкими пылинками, будет пропорционально слабее, но зато встречаются они гораздо чаще. По-видимому, средняя масса частиц межзвездного пылевого вещества лежит в области 10−9—10−11 г, причем средняя плотность этого вещества в Галактике порядка 10−25 г/см3. При скорости в 0,866c поток пыли на корпус корабля составит около 2,6·10−15 г/см2·сек. Это соответствует потоку энергии в 3,4 кал/см2·мин, т. е. почти вдвое превышает солнечную постоянную [прим.]. Если принять, что полная поверхность корабля в 20 раз больше его торцовой поверхности, а излучательную способность взять на порядок ниже, чем у абсолютно черного тела, то равновесное состояние наступит при температуре оболочки, близкой к 100°С. Повышение же концентрации пыли в 10 раз против среднего значения приведет к разогреву [прим.] корабля до 400°С.
Кроме пыли и микрометеоритов, на корабль будет налетать поток межзвездного газа, в основном — водорода, средняя плотность которого в Галактике на порядок больше, чем пыли: примерно 1 атом водорода на 1 см3 (около 10−24 г/см3).
Можно поставить вопрос, при какой скорости целесообразно использовать прямоточный фотонный двигатель [прим.], в котором «сжигание» встречного газа даст энергию, позволяющую компенсировать сопротивление этого газа движению звездолета. Допустим даже, что это удалось сделать. Не меньшая трудность, как нам кажется, лежит совсем в ином направлении.
Поток первичных космических частиц, падающих на Землю (слева) в 1010 раз слабее потока, который встретит космический корабль (справа)
Для релятивистского корабля межзвездный водород становится потоком протонов с энергиями, превышающими 1 млрд. эВ, т. е. потоком космических лучей, причем интенсивность этого потока порядка 1010 частиц на 1 см2 в 1 сек. Напомним, что для нерелятивистского наблюдателя интенсивность первичных космических лучей составляет всего лишь 2 частицы на 1 см2 в 1 сек. Следовательно, допуская даже, что процессы разрушения или нагревания звездолета каким-то способом предотвращены, мы остаемся перед лицом этого колоссального, превышающего в 1010 раз обычную «норму» космического облучения, способного мгновенно убить все живое.
* * *
Из сказанного вытекает, что вопрос о достаточно эффективном двигателе отнюдь не является единственной существенной проблемой, стоящей на пути к релятивистской астронавигации. Не менее важно изыскать способы «очистки» космического пространства перед звездолетом, т. е. устранения с его пути всевозможных микро- и макрочастиц, или какие-либо иные методы защиты от них. Эта задача представляется нам не менее трудной, чем создание фотонного двигателя.
Е. Зингер. К механике фотонных ракет, ИЛ, 1958. [назад]
Речь идет о преобразовании Лоренца, которое связывает отсчеты координат и времени (х, у, z, t) в покоящейся системе К с соответствующими величинами (х', у', z', t') в системе К', движущейся с относительной скоростью υ. При относительном движении по общей оси х эти преобразования имеют вид:
Это значение взято лишь потому, что оно упрощает расчет. [назад]
Для звезд, от которых в неподвижной системе К
излучение приходит под углом α = 90°, эффект Допплера дает в системе К'
укорочение волны в раз. Для звезд, от которых излучение приходит под таким углом а, что cos α = β, в системе К' излучение придет под углом α' = 90°, и получается так называемый чисто поперечный эффект Допплера — удлинение волны в
раз. (Эффект называется поперечным потому, что наблюдатель
К' видит звезду в направлении, перпендикулярном к направлению движения. Это чисто релятивистский эффект). Наконец, волны,
приходящие от источников, находящихся точно позади звездолета, станут длиннее в
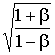раз, а от расположенных прямо перед звездолетом во столько же раз короче.
[назад]
Продольное сокращение длин происходит в отношении : 1, так что у эллипсоида будет именно такое соотношение осей.
[назад]
В сечении плоскостью рисунка получится эллипс.
Его полуси равны ρ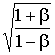
и ρ (в нашем примере это 3,78 ρ и ρ, кривая
а на рис. 6). Центр этого эллипса удален по оси
x на расстояние, кажущимся образом увеличенное по сравнению с истинным расстоянием
s = υ | t | в 
раз, и, соответственно, приближается к наблюдателю с видимой скоростью
(т. е. в
нашем числовом примере 7,47 υ). [назад]
Полуоси эллипса равны ρ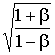
и ρ (в нашем примере это 0,27 ρ и ρ, кривая
б на рис. 6). [назад]
Центр эллипса при этом отстоит от наблюдателя
не на s = υt, а на 
и удаляется со скоростью
. [назад]
См. Т. Terrell. Invisibility of the Lorenz Contraction. «Phys. Rew. Letters», vol. 3, 1959, № 10, p. 501. [назад]
Солнечной постоянной называется число калорий, получаемых квадратным сантиметром поверхности, перпендикулярной к солнечным лучам и находящейся на границе земной атмосферы. В среднем она равна 1,94 кал/см2·мин. [назад]
Впрочем, вопрос о степени нагрева корпуса ракеты довольно сложен, так как возможна значительная потеря энергии на рентгеновское излучение. [назад]
См. J. R. Pierce. Relativity and Space Travel «Proc. Inst. of Radio Eng.», vol. 47, 1959, № 6, p. 1053. [назад]
Источник:
Природа. 1960. № 4. С. 64-70.